![]()
One reason for transforming features is to correct geometrical distortions. If a house has been entered into the database at a wrong location, we can shift it to the proper position. If the scale and orientation are also wrong, then more involved transformations will have to be applied. This kind of geometrical correction is particularly useful when integrating data from other sources of different quality.
In performing any transformation, we need control points. We have explained earlier that a control point is used to relate two coordinate systems, and it has known positions in both systems. Control points can also be used to transform features from one position or shape to another in the same coordinate system. In either case, the idea is the same - if we know the before and after positions of some critical points of a feature, then the changes in shape or position can be determined.
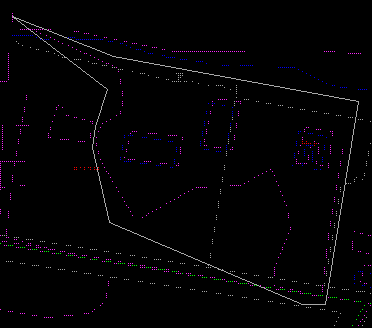
We will use geometrical transformations to show how to fit features from one database to another. Let us suppose we would like to copy the outline of the wooded area from the Ntdb file to Fton. The Fton database, being of larger scale and higher resolution, can be regarded as more accurate.
We notice the difference in location of the same building in the two databases. We will assume that all other features, including the wooded area outline, are distorted in a similar manner. The correct building corners (from Fton) being more accurate and the distorted ones (from Ntdb) can serve as control points to compute the type and magnitude of distortion. We can then apply the same transformation to the wooded area outline to make it conform better to the Fton database.
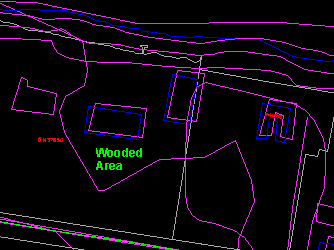
We will do the transformation in several ways, using a different number of control points (house corners) each time. In the first case, only one control point is used, allowing us to shift the features relative to each other. In the second case, two control points are used, allowing us to correct for differences in orientation and scale as well. In the third case, three control points are used. This will correct for shift, orientation, and different scale changes in the x and y directions.
![]() Prepare
the Fton file for the exercises.
Prepare
the Fton file for the exercises.
To ensure that you see the proper features on the Fton file in these exercises, do the following.
1. Open the Fton file and click on the Visibility Parameters
button in the Editor Tools Panel or select the Options > Display > Visibility Parameters ... menu item to exclude contours from the display.
2. Exit from the editor.
![]() Use
one control point to transform.
Use
one control point to transform.
We will use the geometrical transformation command to shift the features
on Ntdb_ste to make them fit better with those on Fton.
1. Open the file Ntdb_ste.
2. Use the File > Management > Add menu item to load the file Fton. Remember to refresh the screen to see both files.
3. Use the Group > Define Group menu item to form a group containing buildings and the wooded area outline we want to copy.
(287980, 740600), 1:1500
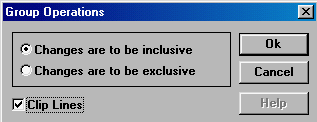
4. Use the Group > Geometric Trans menu item to perform a geometric transformation.
5. Select the inside features to be transformed, turn on Clip Line, and click on OK button.
6. The features to be transformed will be highlighted. Click on the left mouse button to confirm.
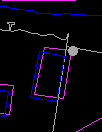
7. Select one of the corners as a control. You might want to use the search option to point precisely at the corner.
8. Point to the correct location of this corner.
9. You can enter more than one control points. In this example, we are using only one. Click on the right mouse button to finish entering the control points.
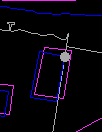
10. The transformed data will be highlighted. Press the left mouse button to confirm.The differences in position of the three buildings affected give an indication of the effectiveness of the transformation. Notice that the middle building which previously crossed the parcel boundary has now been moved back to the proper parcel.

![]()