It is not really necessary to hand pick these points if the file has been topologically structured because the system would have known which points make up which arcs, and which arcs make up which polygons. It would then be possible to simply identify the polygon of interest and let the system retrieve the points forming its outline to complete the area calculation.

In fact, the relating of arcs to polygons and the calculation of their areas has already been performed by the topology building module called the topology builder. In this GIS, the areas computed are stored as one of the system-defined attributes. Hence an area calculation on a topological database is simply a retrieval operation. Unlike the manual method we have used before that involved a lot of pointing on the screen, retrieving the area of a polygon from a topological database involves only pointing at the inside of the polygons.

Retrieve area of a polygon.

NOTE :  Before beginning this section center the map at (288706, 740328), with a scale of 1:500

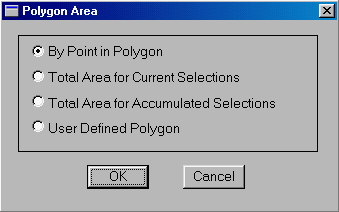
1. Pick the MapQuery > Polygon Area ... menu item.

2. Turn on the By Point in Polygon switch.  This allows you to retrieve a polygon by pointing at its inside.

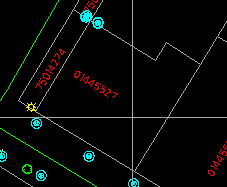
3. Point at the polygon for which you want to retrieve the area. The polygon will be highlighted for your confirmation.

(288706, 740328), 1:500

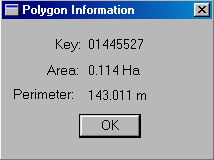
4. The pre-computed area (and perimeter) of the polygon will be retrieved.

Is the area and perimeter measured on a flat map?

Use the MapQuery command to determine whether the area and the perimeter are computed on a flat or an ellipsoidal surface.

Search for the polygon at which the user is pointing.

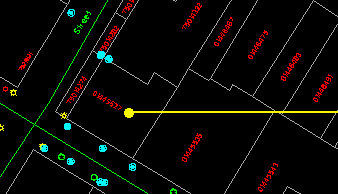
On a line map there are points, lines, and areas. The areas are enclosed by lines. When we point at a polygon, we normally point at its inside. Pointing at its outline is ambiguous because two polygons share the same boundary.

The problem is: given the coordinates of the crosshair, determine which polygon in the database encloses that point. This operation, called the point-in-polygon operation, is one of the most fundamental in a GIS.

Here is one solution. Extend an arbitrary line from the point to the edge of the database. The line can be extended in any direction, but one which is parallel to the axes is easier for the computations. Then we perform intersection tests on this line with all the arcs in the database.

(288706,740328)

Of all the intersections found, determine which one is closest to the point. For example, the arc highlighted below contains the closest intersection. That arc has a direction as indicated by the arrow.

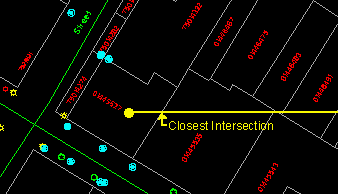
In the topological database, the polygon to the left of this arc has already been identified as 01445535 and the one to the right as 01445527. You can verify this by displaying information on this arc. The final step in the solution is to determine if the point is to the left or to the right of this arc. We will not elaborate on the method here except to point out that the calculations involved are not complicated.

It is a tedious process to perform intersection tests on all arcs in the file to find the closest intersection. But this cannot be avoided unless a spatial indexing system is in place to help minimize the number of such tests.

We have described earlier, in the chapter on Coordinate System and Distance Measurement, a spatial indexing system that logically divides the database into regular cells. This structure, if used on a database of arcs, can tell which arcs fall inside which cells. In the intersection test, we first locate the cells containing the point and the extended line, which are those shaded in the following diagram.

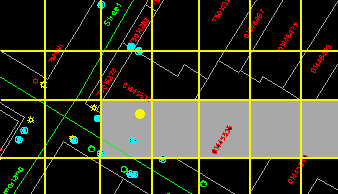
All arcs falling outside the shaded area can be immediately excluded from the intersection test, thus reducing the number of calculations required.