In the database we are using, the resolution has been set at 0.05 metre (or 5 cm) on the ground. This is called the ground resolution and is specified by the user when creating the database.

This fine resolution has little effect on the display unless a very large scale is used. The following tree symbol can be found at (289157, 740029), and the display scale is 1:80.

(289157, 740029), 1:80

At a scale of 1:20, the effect of resolution on the image is quite noticeable.

1:20

When we enlarge the image to 1:10, the staircase effect due to resolution is large enough to be measured with accuracy.

1:10

Verify the length of the straight segments.

Use the MapQuery > Distance Between 2 Points menu item to verify that the short straight segments are indeed 0.05 metre long.

Visualize the resolution grid.

We mentioned earlier that you can read the coordinates at any location on the display. This is not entirely true, because there are locations that you cannot point at. To illustrate this, we have to zoom into the database at high magnification.

Centre at (289156, 740030), and choose a scale of 1:10. Select the MapQuery > Point Location menu item, and read the coordinates at various locations that are very close together. Recall that every time you select a point, the location at which the coordinates were read will be marked by a cross. At this high magnification, you will notice that where you point is not necessarily where the marker will appear. By pointing at several locations that are very close together, you would have left behind a series of markers that form a regular grid on the display. If you are patient enough, you could generate a grid that covers the entire database. This grid would indicate the only places at which you can read coordinates.

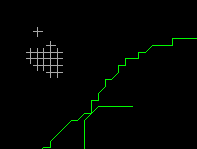
(289156, 740030), 1:10